笔记:两点透视
- 两点透视(Two point perspective)
- 旋转消失点(rotating the vanishing points)
- 定位测量点(locating the measure points)
- 构造一个2点透视的立方体(constructing a 2PP cube)
- 如何绘制非常远的消失点(who has a 12 foot table?)
原文地址:https://handprint.com/HP/WCL/perspect3.html
系列笔记:
两点透视的整体主题是,通过将消失点旋转特定角度以及在合适的measure bar上确定相应的measure points以便投射所需的深度等办法,确定物体在两点透视中的正确比例。
两点透视(Two point perspective)
两点透视的标志性特征(Defining Features of Two Point Perspective)
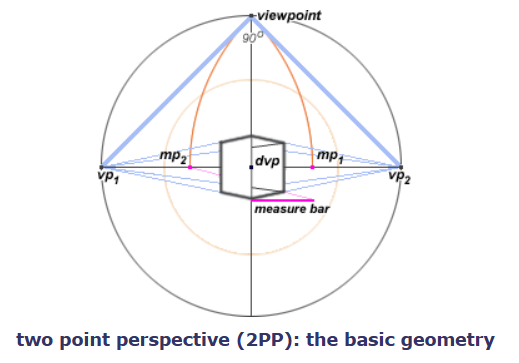
下图展示的是最简单的两点透视,一个正方体以相对画面45度角的方式摆在画面中心。
两点透视的物体有两个消失点(vp1和vp2),两者之间是90度。每个消失点与direction of view之间的夹角不同,但是两者之和永远是90度。沿着物体的2个消失点的方向上的深度变化是由2个测量点(mp1和mp2)来决定的。通过测量点,我们可以将measure bar或者单位长度投射到物体2个消失点所在的方向上。
旋转消失点(rotating the vanishing points)

在视觉射线法中,我们通过物体的旋转角度(angle of rotation)来定位物体的左右消失点,该角度等于物体正面与画面之间的角度,也等于物体侧面与direction of view之间的角度。通过将物体在仰视图中离观察者(viewer)最近的那个角与向上翻折的viewpoint重合,我们可以确定物体的旋转角度(angle of rotation)。接下来将物体的两边从viewpoint延长与画面相交(同时也是与地平线相交)便可以确定物体的两个消失点。
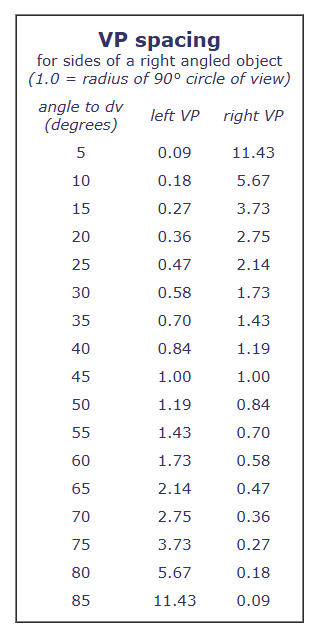
VP定位速查表
举例来说,假设一个正方体左侧面与direction of view的角度是30度,那么通过VP定位速查表可以得知vp1应该在地平线左侧从direction of view开始的0.58个半径长度的位置。此时正方体右侧面与direction of view的角度是60度(90-30度),对应的vp2的位置则是在地平线右侧从direction of view开始的1.73个半径长度的位置。
定位测量点(locating the measure points)
在一点透视中,单个消失点(principal point)决定了空间中沿着纵深线(指向principal point的消失线)方向上的透视变化,而对角消失点则可以将单位长度从图像平面映射到纵深方向上。
在两点透视中,principal point仍然定义了观察者的纵深方向的透视变化,以及direction of view在地平面和所有平行于视线方向的平面上产生的透视梯度。但物体本身的消失点却在两个不同的方向上(即两条消失线上)发生着各自的透视变化,我们的任务便是在这2条消失线上建立单位刻度。
测量点的几何原理(Geometry of Measure Points)
在视觉射线法中,解决这个问题的办法是将地线(ground line)上的度量单位映射到透视空间中物体消失点所在的方向上。
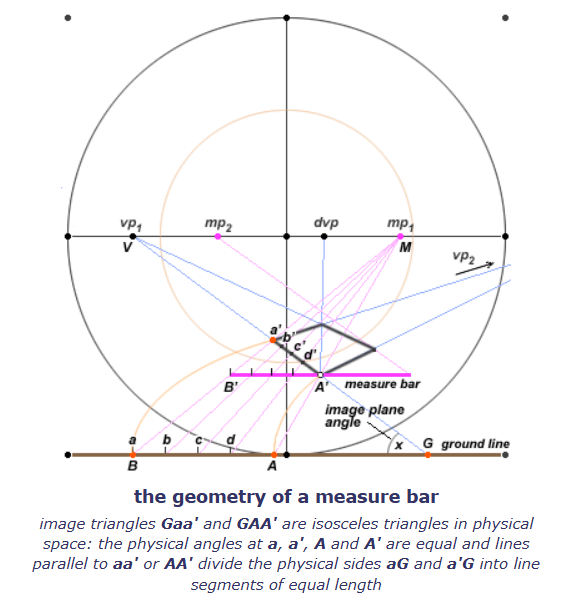
假设我们在物理空间中(注意,不是在画面中)以G为顶点GA’为半径构造出一个弧线,它与地线在A点相交。由此得到的A’GA便是一个等腰三角形,而GA’在物理空间中的长度等于GA。A’A的延长线与地平线的交点便是消失点vp1的测量点mp1。
这个构造所达到的效果是所有平行于A’A的线之间的间隔在地线(ground line)上的长度与在消失线上的长度相等。举例来讲,线条aa’和bb’是2条平行于A’A的线,这2条线在地线上的形成的线段ab的长度与物理空间中的线段a’b’是完全相等的。
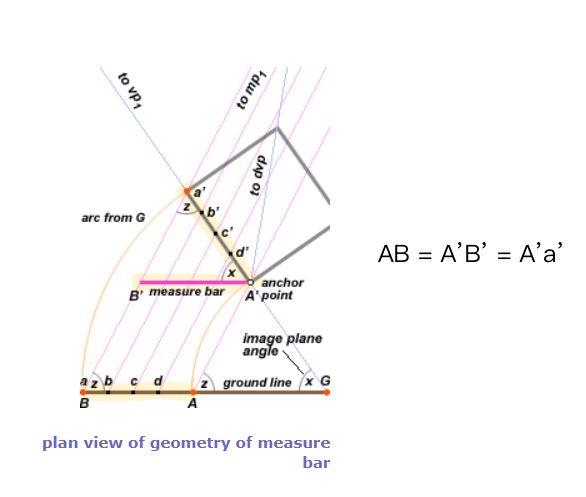
由俯视图可以看出,线段AB与线段A’B’(即measure bar)以及消失点方向上的线段Aa’三者之间的长度相等的(因为AB与A’B’是菱形的两条边,而A’B’与Aa’是等腰三角形的两条边)。
定位测量点(Locating the Measure Points)
那么实际操作中该如何定位测量点呢?显然我们无法直接在画面上G为顶点画一条圆弧,因为透视的关系,物理空间中的一条圆弧会在画面中变成一个椭圆的圆弧。
其实想要定位测量点有一个非常简单的办法,只需以物体的某一个消失点为顶点从向上翻折的viewpoint画一条弧线与地平线(或者说是与图像平面)相交,得到的交点便是这个消失点的测量点。这条弧线其实就是在仰视图中在viewpoint和图像平面之间构造出了一个等腰三角形。
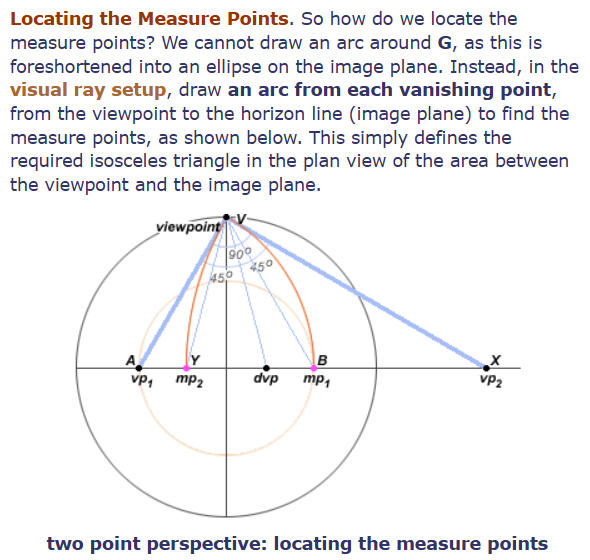
因此,从 vp1 出发的圆弧与图像平面相交于 B 点;三角形 VAB 是平面仰视图中的在视点和图像平面之间的一个等腰三角形(此时相当于将其沿地平线向上翻折到90°视圈上),其底边 VB 与图像平面相交于测量点 mp1。从 vp2 出发的圆弧与图像平面相交于 Y 点;三角形 VXY 是一个等腰三角形,其底边 VY 与像平面相交于测量点 mp2。
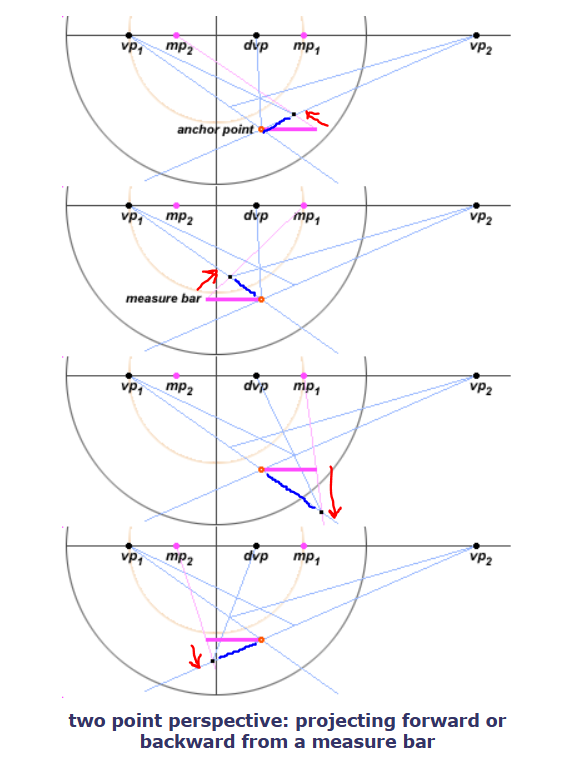
两点透视中如何正确地将measure bar映射到消失线上更靠前或靠后的位置
相比于一点透视,在两点透视中使用measure bar时我们需要更加谨慎一些。在两点透视中,将measure bar放置在图形的哪一边,以及使用哪个测量点都很重要,因为此时物体的每一侧都有各自独立的测量点。
一个基本的原则是:你是在把度量单位映射到消失线(vanishing lines)上,而消失线会汇聚到一个消失点(vanishing point)。因此,你必须使用以该消失点为顶点的圆弧所确定的对应测量点。这个测量点位于你所要映射度量单位的那条消失线的消失点的对面一侧。
上图展示了两点透视中将放在基准点两侧的measure bar映射到消失线上时可能出现的四种组合情况。在所有情况下,正确的测量点总是那个需要测量的消失线的消失点所对应的测量点。测量点的选择并不是由measure bar在基准点的左边还是右边决定的。还要注意,measure bar上的点既可以向后投射(靠近地平线的方向),也可以向前投射(靠近观察者的方向);来自对角消失点(dvp)的视觉射线可以验证这些向前的映射。
如何使用量角器精确确定消失点的旋转角度
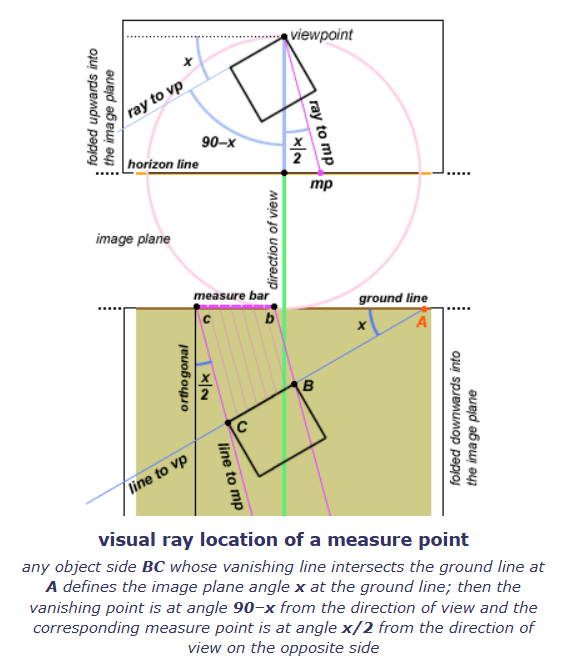
你可以使用量角器(将其中心放置于viewpoint上)来精确确定消失点的旋转角度。物体某个侧面相对于图像平面旋转的角度等于 该侧面的消失点与viewpoint的连线 以及 通过viewpoint的一条水平线(图中虚线) 之间的夹角(在下图中标记为 x)。
而该物体侧面的消失点(vp1)则位于距direction of view方向(dv)90−x 度的位置,而它的测量点则位于距 direction of view 方向 x/2 度的位置,且处在direction of view的另外一侧。举例来说,物体的正面 BC(在平面仰视图中所示)相对于图像平面旋转了 30°;因此 x = 30°。这意味着 vp1 将在视线方向的一侧偏转 60°,而它的测量点 mp1 则位于视线方向右侧 15° 的位置。无论物体相对于图像平面如何旋转,这些对应关系始终成立。
构造一个2点透视的立方体(constructing a 2PP cube)
一旦你定位了两个消失点和两个测量点,在2点透视中构造立方体或长方体的步骤与在1点透视中相同,唯一不同的地方是还需要measure bar来确定物体正面的两个侧面的具体位置。
构造2点透视的具体步骤是:
- 确定画面中的anchor point和anchor line;
- 将anchor line的2个顶点与2个vanishing points相连(对应立方体侧面的四条边);
- 绘制2个measure bars,其长度分别对应立方体正面的两个侧面各自的宽度(如果该立方体是正方体,则measure bar的长度等于anchor line的长度),将2个measure bars的一端与anchor point重合,分别摆放于anchor point的各一侧(measure bar具体摆放规则参考前文“如何正确地将measure bar映射到消失线上更靠前或靠后的位置”);
- 沿着两条measure bar远离anchor point的那一端分别各画一条连到其对应测量点的直线(该直线与消失线的交点即为立方体两个侧面的对应深度);
- 沿着2个交点各画一条垂直于地面的直线,与上方的消失线相交(所得到的线段为立方体两个侧面的后面两条边,其长度均小于anchor line);
- 将立方体两个侧面的后面两条边的2对上端点和下端点与对侧的消失点相连(这些线的交点即为立方体第4条垂直边的上顶点和下顶点);
- 将4条垂直线段的相邻顶点用直线相连。
至此得到2点透视画面中的立方体。
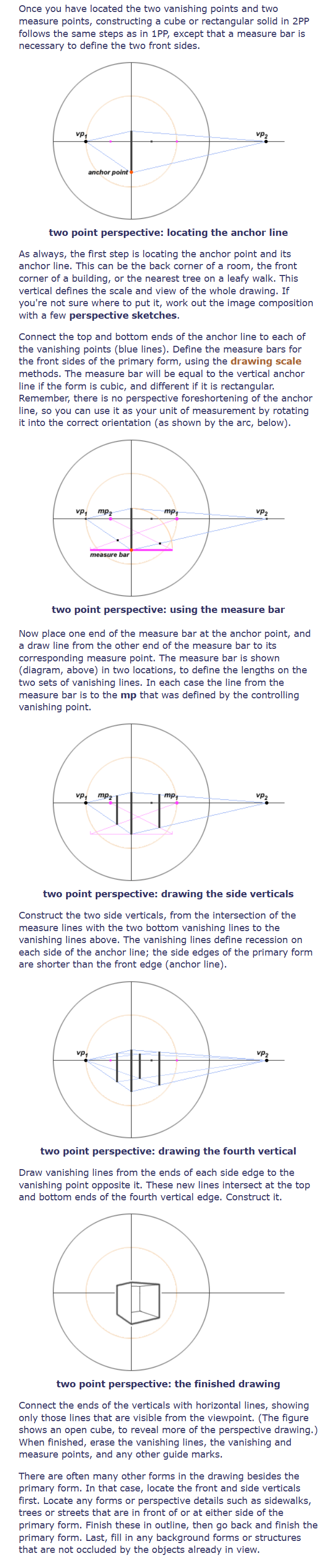
如何绘制非常远的消失点(who has a 12 foot table?)
Unfortunately it is fairly common to start with the primary form in an orientation that puts the two vp’s inconveniently far apart. In the previous cube construction example, assuming a 10 foot circle of view, the cube is oriented so that the two vp’s would about 11 feet apart — one 3.2 feet to the left of the dv, and the other 7.7 feet to the right. This isn’t very convenient for a drafting table.
If those alternatives don’t appeal to you, then you can rescale the drawing.
How do you define the crucial distance dc (from the direction of view to a vanishing point) in the first place? The easiest method is to use my vanishing point calculator to get the measurements of the vp’s and mp’s, and adjust the viewing distance to the object and your angle of view until you get the proportions that seem desirable.
Or, as described above, you can reduce the circle of view to a workable size, use the method for rotating the vanishing points to determine the locations of vp1 and vp2, measure the distance from these to dv on the diagram, then scale those distances back to life size.
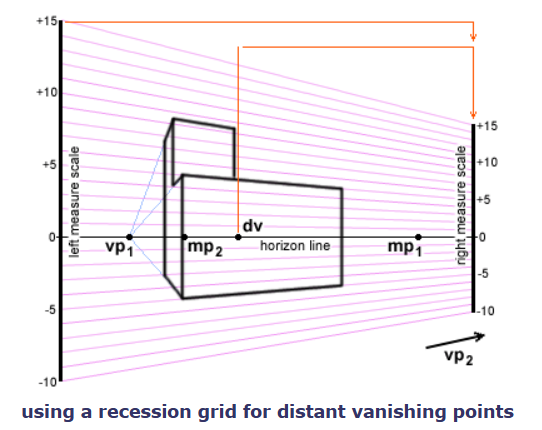
Unfortunately this method, even after you get the hang of it, still forces you into a lot of poking of a pocket calculator, and is hopelessly tedious and prone to error if many lines must be inserted in your drawing. The ultimate solution is to generate a recession grid for the distant vanishing point, and use this grid to determine the perspective reduction for any verticals in the drawing.