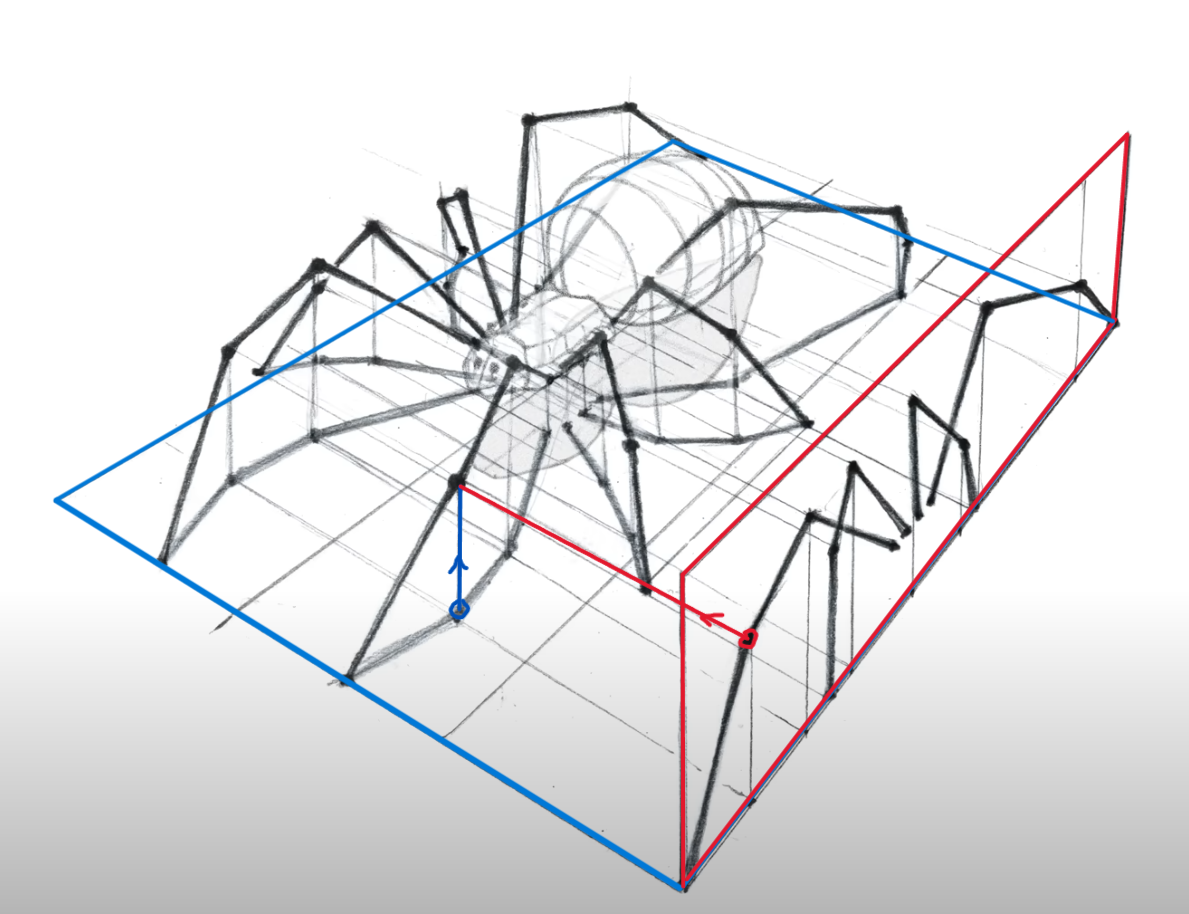
笔记:高级透视技巧
原文地址:https://handprint.com/HP/WCL/perspect5.html
系列笔记:
复杂平面图形的透视画法
圆的透视画法(Projecting A Circle)
不使用平面图来构造圆形的透视(Circle Without a Plan)
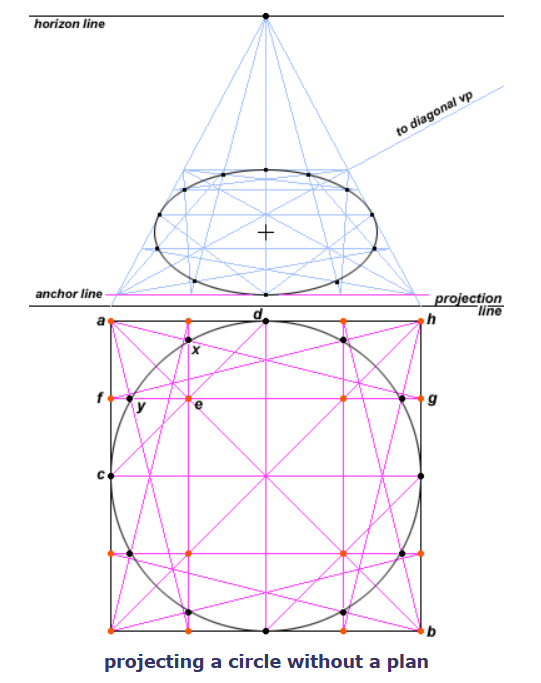
构造步骤:
- 在画面中画出透视的正方形
- 在透视的正方形内逐步构造出图中的辅助线
- 根据辅助线构造出透视中的圆形
使用平面图来构造圆形的透视(Circle With a Plan)
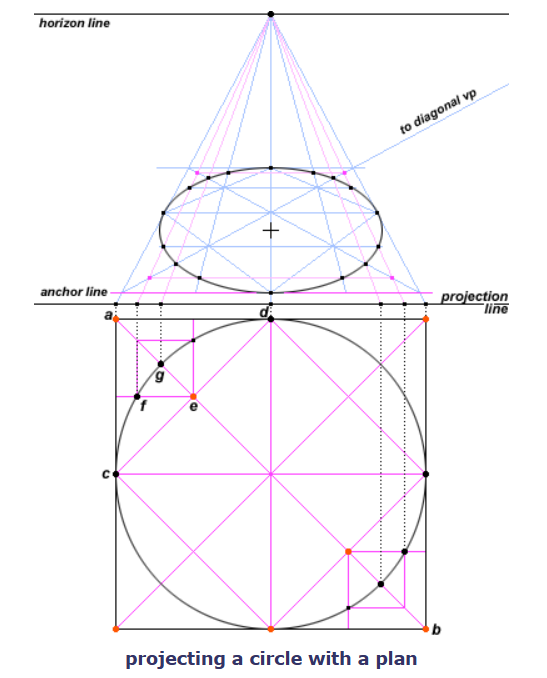
构造步骤:
- 在平面图中画出正方形和内嵌的圆形
- 逐步画出辅助线
- 将正方形和辅助线投射到画面中
- 根据辅助线构造出透视中的圆形
椭圆的构造(Ellipse Construction)
每一个椭圆都可以通过它的高度和宽度来描述,这两个维度分别称为长轴(最长的方向)和短轴(与长轴垂直的方向)。由此可以得到两种简单的椭圆构造方法,以及一种估算圆在透视中缩短程度的计算方式。
根据固定的高度和宽度来构造椭圆的3种方法
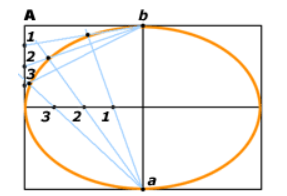
在 第一种方法(A) 中,高度和宽度先定义一个矩形,然后用两条线将矩形等分为四个象限。接着,将矩形内部的一条水平线段(相当于椭圆的长轴)和矩形外部的一条垂直线段(长度等于椭圆的短轴)按同样的比例划分为相等的部分(这些点之间不必保持相等的间隔距离,只需这些点在两条线段上的比例相等即可,比如均为所在线段的4分之一长度)。然后,从中线上的两个点 a 和 b 分别向这些分点引线,如图所示。对应直线的交点定义了椭圆在一个象限中的点。最后,将这些关键点用徒手曲线或曲线板分段连接,并复制到其他三个象限中,即可得到完整椭圆。
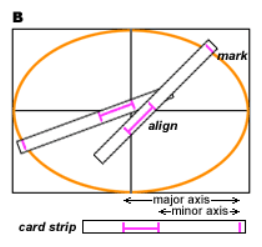
另一种更高效的方法是游标法(Trammel Method,方法 B)。
具体做法是:先确定椭圆的外接矩形,然后将长轴和短轴的长度转移到一条硬纸板或厚纸条上(保持长短轴的某一端对齐,见右图)。由于长轴和短轴长度不相等,在另一端会留下一个间隔(洋红色线所示)。将这两个端点分别与椭圆矩形的短轴和长轴对齐,此时便可以直接在纸条另一端的对齐点标记出椭圆的圆周所在的位置。此方法快速,但当长轴和短轴逐渐接近相等(即椭圆趋近圆形)时,精度会显著下降。
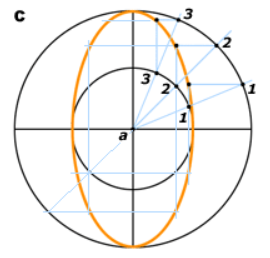
第三种方法(C) 使用两个以点 a 为圆心的同心圆。
先画出大圆和小圆,然后用两条互相垂直的直线将其四等分,这两条直线定义了椭圆的长轴和短轴。接着,从点 a 向外任意画若干条放射线,使它们分别交小圆和大圆,得到成对的交点。然后从这些交点分别作平行于椭圆的长轴或短轴的线段;这些线的交点便是该椭圆在这个象限内所在的点。此方法的优点在于:如果将“辐射线”以及水平、垂直辅助线延伸穿过整个大圆,就能标定出完整椭圆的全部圆周。
然而,这里出现了一个问题。从下面的圆形构造图可以看出,椭圆的中心并不与图像方形的中心(即方形对角线的交点)重合,因为透视缩短导致方形的后半部分看起来比前半部分略小。因此,表示椭圆中心的黑色十字并没有位于对角线交点,而是稍微偏下(靠前)的位置。
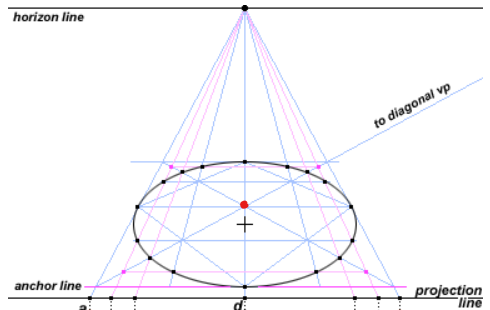
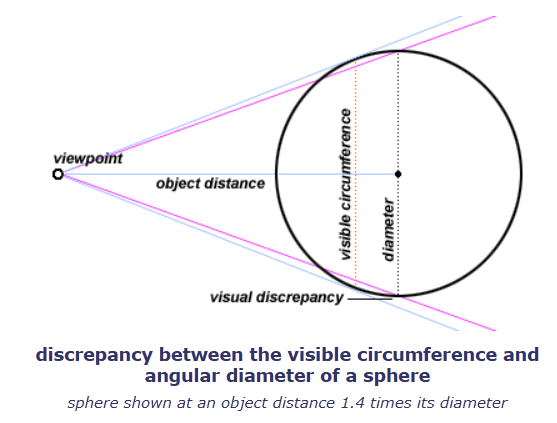
这与另一个视觉差异本质相同:球体的可见宽度(等于椭圆长轴在图像中的宽度)与球体直径的视觉角度(等于透视方形中横跨中心的宽度)之间的差异(见下图)。这个问题会在下面“球体投影”章节中进一步讨论。遗憾的是,除了在平面图中按比例绘制外,没有一种简单的方法能直接缩放椭圆的宽度,因为椭圆的长轴并不与正方形的中心横截线重合,而椭圆与正方形边框相切的点通常也不位于椭圆的长轴上。但在小于20°视角范围的透视圆中,这种误差极小,可以忽略不计(这里的视角范围不是指下文提到的椭圆自身的角度,而是椭圆在画面中的视觉角度,这与椭圆的大小以及其与画面距离有关,不是固定不变的;而下文提到的椭圆自身的角度对同一个椭圆而言是一个固定值,有相关的定义,不受观察距离影响)。
这也是为什么建筑师们通常习惯使用椭圆模板以及依赖于计算机绘图软件的一个主要原因。椭圆模板包含大量切割好的椭圆,每一个都比前一个略大,并且都按照一个标准视角比例缩放,适配到包含圆的平面。绘图者只需选择与所需长短轴比例最接近的模板角度,然后再挑选最符合图像大小的椭圆切口即可。
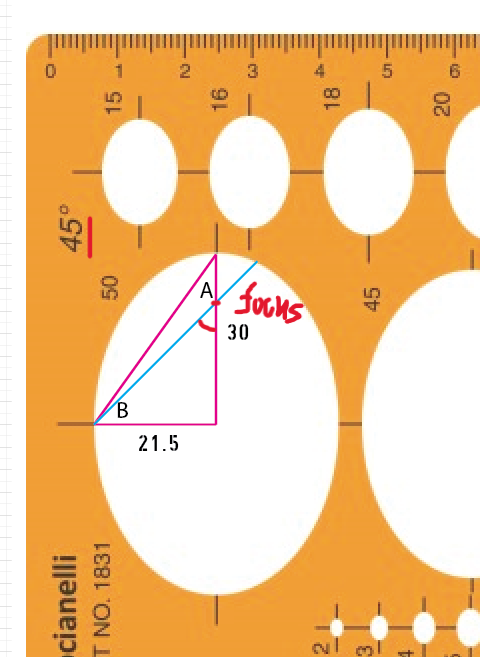
椭圆模板角度的定义是椭圆焦点到短轴顶点的连线与长轴之间的夹角。注意这里的角度虽然也是通常范围从 0°(一条平直的线)到 90°(一个完整的圆),但它与该椭圆在透视画面中的视觉角度(angle of view)是两个完全不同的概念。以下图蓝色的45°椭圆为例。首先,将一段长度与长轴相等的线段的一端与短轴顶点重合、另一端与长轴相交,根据椭圆焦点的公式(长轴^2 = 短轴^2 + 焦点到圆心距离^2)可知,相交得到的点即该椭圆的焦点。椭圆模板的角度指的就是这条线段与长轴之间的夹角。图中显示该椭圆长轴为30,短轴为21.5,根据椭圆公式可以求得焦点距圆心距离也等于21.5(这里是一个等边直角三角形),进而可以求得焦点与短轴的连线与长轴的夹角,即椭圆的角度为45度。
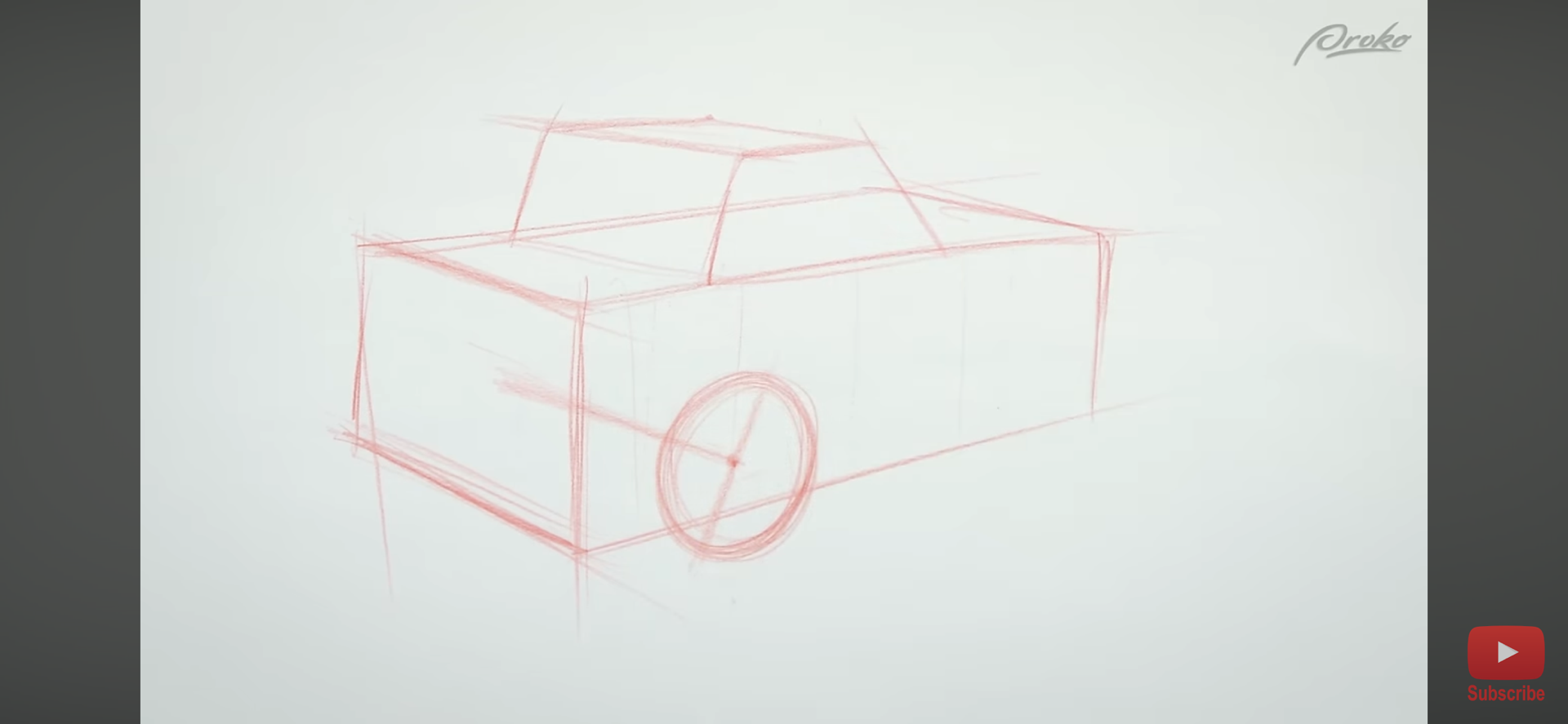
如何画透视中的圆(即找到椭圆的长轴和短轴)
在一个proko视频里学到一种简单的找到透视中圆形(即椭圆)的长轴和短轴方向的办法:
- 画一条垂直于圆所在平面的透视线条,该线条与椭圆的短轴平行;
- 在画面上画一条垂直于短轴的线条(注意,这里是画面上的垂直关系,直接用量角器和直尺即可确定),该线条与椭圆的长轴平行;
- 可以根据包含该圆形的正方形大致确定椭圆的圆心,以及长轴和短轴的长度(只是大概,不是精确,原因如上文所述)
评论里提供了一个对此方法的直观理解:
A good way to visualize the car wheels trick is to think of the left and right wheel as forming a cylinder bwtween them. And the reason the circle of the wheels is squished along that perpendicular axis is because the more you tilt the cylinder in perspective so you see it from the side, the more those top and bottom plane circles of the cylinder become squished into a line that’s perpendicular to the height of the cylinder.

人体透视
艺术家在透视绘画中遇到的最困难的问题,无疑是人体。但这也是最早被尝试解决的问题之一。一个复杂但精确的方法见于皮耶罗·德拉·弗朗切斯卡的《论绘画透视》(De Prospectiva pingendi,约 1474 年),而阿尔布雷希特·丢勒在《人体比例四书》(Vier Bücher von menschlicher Proportion,1528 年)中则提出了比较粗糙但高效的方法。16 世纪时,这个问题真正“火热”起来——因为大量天顶壁画里那些飞向天堂的圣徒与天使需要仔细分析人体的透视缩短(包括人的脚底)。到 17 世纪,这类研究已成为绘画学习的常规课程,追随丁托列托的创作风格。
将人体进行透视的最简单的方法是:先通过写生或或临摹一张合适角度和姿态的照片。然后把这幅人物作画按比例缩放到所需大小,并描摹到画面上的指定位置即可。
使用观察网格进行透视绘制
一种更严格更“较真”的方法是:将人体的三维点映射到透视空间里。传统上大体有三种方法:
- 截面投影法 (sectional projection)
- 体块投影法 (volumetric projection)
- 骨架投影法 (armature projection)
截面投影法 (sectional projection)
皮耶罗使用的就是截面投影法:他将人头划分为一系列平行的矢状面,然后像我们之前投射八边形平面那样,把每个截面的关键点投射出来。只不过这里的这些方格在垂直方向上的间距要与解剖学上各截面之间的实际距离相对应。这样就形成了一个由点构成的“笼子”,最后只需把这些点还原为面部特征,就能重建出整张脸。
体块投影法 (volumetric projection)
第二种方法是体块投影法:它先把人体分解成一系列相互连接的椭圆体、圆柱体、方盒子或棱锥,然后在透视中投射这些简单形体的主要棱角或轴线,接着再围绕它们重建人体。这种方法在巴洛克时期很流行,甚至一直延续到 20 世纪的人体绘画和透视教材中。我非常不喜欢这种方法,因为它彻底破坏了人体那种富有张力、关节灵活、又浑圆有力的特征。我认为,积极的人体写生绘画训练才是更好的方法,它能让人从不同角度真正理解身体的形态与重量感。
骨架投影法 (armature projection)
如果你已经具备了对人体的基本理解,那么骨架投影法就是一个非常高效的方式,可以在透视中把握人体比例。你真正需要的,只是一个在美术商店里随处可见的那种木制人体模型。
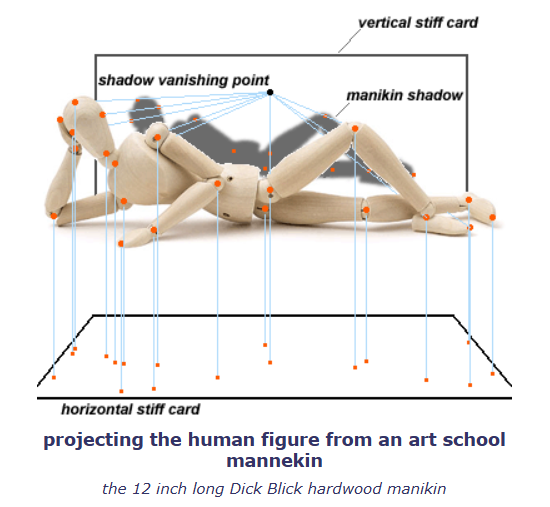
上图展示了这种方法的基本步骤:
- 先把木偶摆放成所需的姿势,然后把它放在玻璃桌面或投影架上。用天花板灯或尽可能高处的聚光灯,把木偶的影子投射到人物下方的一块硬质白卡纸上。利用影子作为参照,在卡纸上标记出主要关节的位置。
- 接着,在木偶的一侧、与木偶等高、并且与人体主轴成直角的地方,放置一盏聚光灯或台灯,距离要和天花板灯与木偶的距离相同。然后在木偶身后,支撑另一块硬质白卡纸,距离与先前下方卡纸相同。用同样的方法标记出关节的位置。
- 从这两张卡纸中选择其中关节间距更合理的一张卡纸作为主视面,把关节点要么描到方格纸上,要么直接使用卡纸进行测量:测量从每个点到卡纸的一条长边和一条短边的距离(作为X轴和Z轴的比例数据)。再从另一张卡纸上,取一组点到其长边的距离(作为Y轴的比例数据)。
- 接着,用前面介绍的方法把这些数据缩放、旋转并转移到一个比例尺上,然后投射到透视空间中(的X、Y、Z轴上去)。
- 最后再根据这些关节位置,通过手绘将透视后的身体形态描绘出来。
虽然我用木偶来解释这种方法,但如果能从同一距离拍摄一个姿势的两张互相垂直的照片,这个方法会更好用。测量可以直接在照片上进行,把每张照片看作是一块“投影卡”。在电脑上,用 Photoshop 之类的图像处理软件,你甚至可以先把照片变形、缩放,使之与预先绘制好的透视矩形框相吻合,然后直接在两张照片之间连线对应的特征点,而不必进行任何测量。
艺术家们现在完全可以用 Poser 这样的软件来生成任意姿势的男女“数字木偶”,无论是裸体还是着装,并以此为基础绘制作品。而且还有一系列 VirtualPose 光盘可以用二维旋转的方式呈现静态姿势。针对大型动物的类似软件,相信也很快会出现。